推荐系统模型之DIN
Deep Interest Network(DIN)由阿里妈妈的精准定向检索及基础算法团队在2017年6月提出。 它针对电子商务领域(e-commerce industry)的CTR预估,重点在于充分利用/挖掘用户历史行为数据中的信息。
主要思路
针对问题
第一个问题是目前很多推荐系统模型,都是以 Embedding & MLP 的方法结合,这种方法相对传统机器学习有较好的效果提升,但是存在一些缺点
用户的兴趣通常是多种多样的,而 Embedding & MLP 方法中有限的向量维度会成为用户多样化兴趣的瓶颈,如果扩大向量维度会极大地增加学习参数和计算负荷,并增加过拟合风险;
不需要将用户的所有兴趣都压缩到同一个向量中。比如用户购买了泳镜并不是因为上周购买了鞋子,而是因为之前购买了泳衣
第二个问题,训练具有大规模稀疏特征网络时面临非常大的挑战,比如基于 SGD 的优化方法可以采用 Mini-Batch 来更新参数,但加上 L2 正则化后其计算量会非常大,因为每个 Mini-Batch 都需要计算所有参数的 L2 范式
提出方案
针对这些问题,DIN 模型通过考虑给定候选广告的历史行为的相关性,自适应地计算用户兴趣的表示向量。通过引入Attention机制来实现局部激活单元,DIN 模型通过软搜索历史行为的相关部分来关注相关的用户兴趣,并采用加权总和池化来获取有关候选广告的用户兴趣的表示形式。与候选广告相关性更高的行为会获得更高的激活权重,并且支配着用户兴趣。这样用户的兴趣表示向量就会随着广告的不同而变化,从而提高了模型在有限尺寸下的表达能力,并使得模型能够更好地捕获用户的不同兴趣。
同时作者提出了一个Mini-batch Aware Regularization方法,可以只计算非零特征参数的 L2 范式。此外还考虑了输入数据的分布,设计了数据自适应激活函数Dice,显著提升了模型性能与收敛速度
特征设计
论文中作者把特征分为四大类:用户特征、用户行为特征、广告特征、上下文特征,并没有进行特征组合/交叉特征。而是通过DNN去学习特征间的交互信息
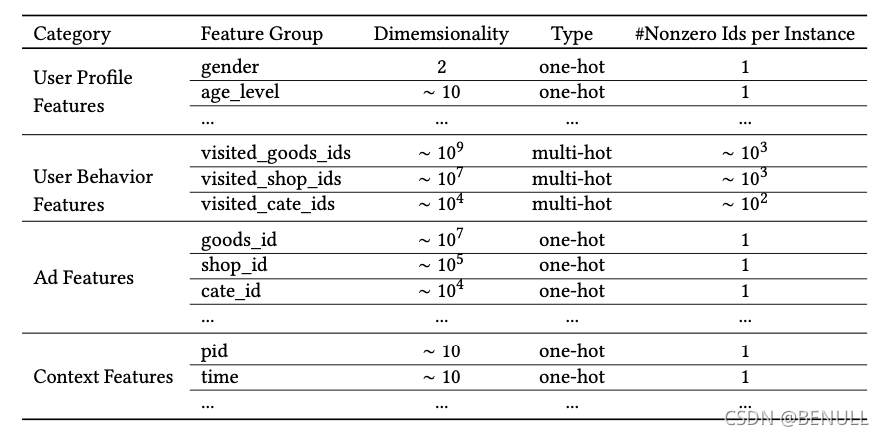
模型结构
基准模型
基准模型结构主要由 Embedding 和 MLP 构成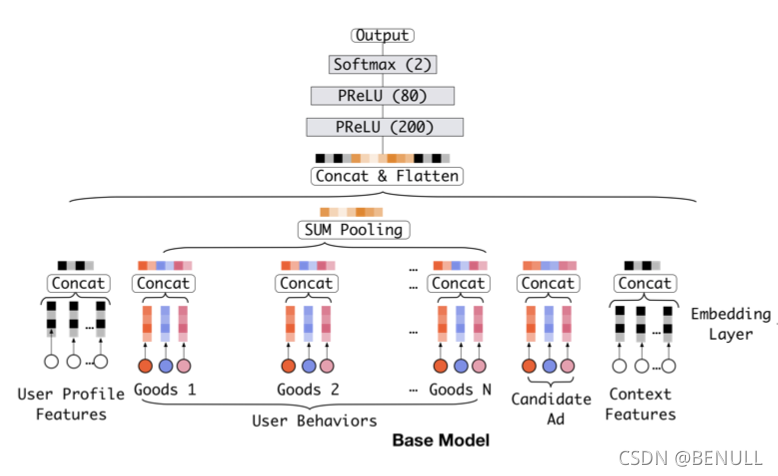
基准模型的一个缺点在于对用户兴趣多样化的表达受限。
基准模型直接通过池化所有的 Embedding 向量来获的一个定长的表示向量。由于表示向量长度固定,表达受到一定的限制,假设最多可以表示 k 个独立的兴趣爱好,如果用户兴趣广泛不止 k 个则表达受限,极大的限制了用户兴趣多样化的表达,而如果扩大向量维度则会带来巨大的计算量和过拟合的风险。
同时在基准模型中,用户行为特征经过简单的池化操作后就送到下一层训练,对于行为中的商品没有区分重要程度,也和广告特征的中的商品没有联系,事实上广告特征和用户特征的关联程度非常强。在建模过程中投给不同特征的注意力应该有所不用,而注意力的得分的计算体现了与广告特征的相关性。
利用候选商品和历史行为为商品之间的相关性计算出一个权重,这个权重久代表了注意力的强弱,在加入了注意力权重后的模型就是DIN
DIN模型
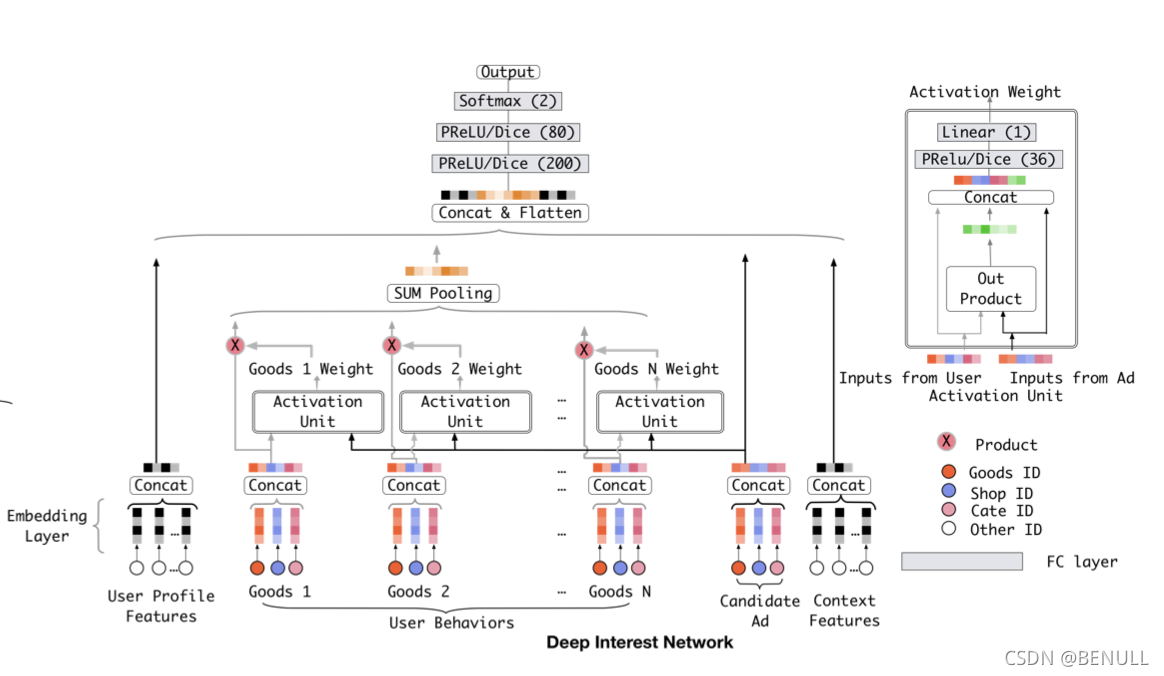
DIN模型模仿了注意力机制的过程,即以给定的广告为出发点,关注相关联的历史行为,在此基础上,DIN会自适应地计算用户兴趣的表示向量,这使得在不同的广告上,这个表达向量也会不同
用户的兴趣表示计算如下
其中$f\left(v{A}, e{1}, e{2}, \ldots, e{H}\right)$表示长度为H的用户U的用户行为嵌入向
$V_A$ 是广告A的embedding vector,这样$V_u(A)$ 随着广告的不同而变化(长度不变,依旧为H)
传统的attention需要对所有的分数通过softmax做归一化,这样做有两个好处,一是保证权重非负,二是保证权重之和为1。但是在DIN中不对点击序列的attention分数做归一化,直接将分数与对应商品的embedding向量做加权和,目的在于保留用户的兴趣强度。例如,用户的点击序列中90%是衣服,10%是电子产品,有一件T恤和一部手机需要预测CTR,那么T恤会激活大部分的用户行为,使得根据T恤计算出来的用户行为向量在数值上相对手机而言更大。
训练手段
Mini-batch 感知正则化
CTR中输入稀疏而且维度高,通常的做法是加入L1、L2防止过拟合,但这种正则方式对于工业级CTR数据不适用,结合其稀疏性及上亿级的参数,以L2正则化为例,需要计算每个mini-batch下所有参数的L2,计算量太大,不可接受。
阿里提出了自适应正则的做法
- 针对feature id出现的频率,来自适应的调整他们正则化的强度。对于出现频率高的,给与较小的正则化强度,对于出现频率低的,给予较大的正则化强度
- 只计算mini-batch中非零项的L2-norm
数据自适应激活函数
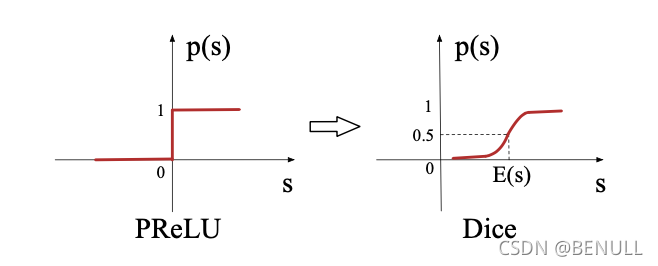
ReLU => PReLU => Dice
PReLU其实是ReLU的改良版,由于ReLU在x小于0的时候,梯度为0,可能导致网络停止更新,PReLU对整流器的左半部分形式进行了修改,使得x小于0时输出不为0。 研究表明,PReLU能提高准确率但是也稍微增加了过拟合的风险。PReLU形式如下:
PReLU函数以0点作为控制转折点,这对于输入层具有不同分布的情况不适用,因此,论文设计了一种新型数据自适应激活函数Dice
主要思想是依据输入数据分布进行自适应调整修正点,该修正点不再默认为0,而是设定为数据均值。其次,Dice的一个好处是平滑过渡两个状态
在训练阶段, $E[s]$和 $Var[s]$是每个mini-batch 的平均值和方差,在测试阶段,$E[s]$和 $Var[s]$随着数据进行移动,$\epsilon$是一个小常数项,设定为 $10^{-8}$
当 $E[s]=0$ and $Var[s]=0$ 时,Dice退化为 PReLU
实现
Model
1 | class DIN(Model): |
Modules
1 | class AttentionLayer(Layer): |