推荐系统模型之DeepFM
DeepFM: A Factorization-Machine based Neural Network for CTR Prediction是华为和哈工大在2017发表的论文,在Wide&Deep结构的基础上,使用FM取代Wide部分的LR,不需要再做复杂的特征工程,可以直接把原始数据输入模型。
主要思路
DeepFM=DNN+FM
因子分解机(Factorization Machines,FM),具有自动学习交叉特征的能力,避免了Wide & Deep模型中浅层部分人工特征工程的工作,通过对每一维特征的隐变量内积来提取特征。理论上FM可以对比二阶更高阶的特征组合进行建模,实际上由于计算复杂度的原因,一般只用到二阶特征组合。
而对于高阶的特征组合,很自然想到利用DNN。但是稀疏的One-Hot特征会导致网络参数过多,通过将特征分为不同的field送入dense层,得到高阶特征的组合。
最终将低阶组合特征单独建模,然后融合高阶组合特征,就是DeepFM了。
模型结构
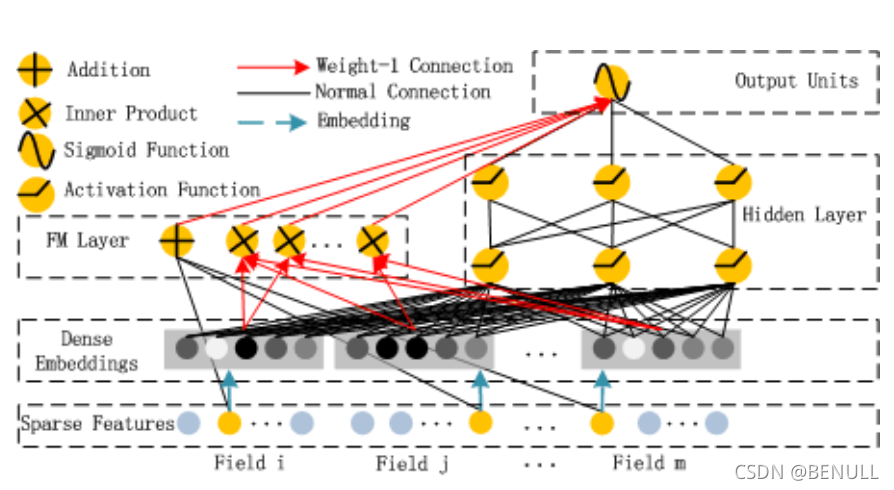
这个模型分为FM部分和Deep部分,和Wide & Deep模型不同的是,DeepFM两部分共享原始输入特征
在输入特征部分,由于原始特征向量大多是高度稀疏的连续和类别混合的分域特征,为了更好的发挥DNN模型学习高阶特征的能力,文中设计了一套子网络结构,将原始的稀疏表示特征映射为稠密的特征向量。
子网络设计时的两个要点:
- 不同field特征长度可以不同,但是子网络输出embedding向量需具有相同维度k;
- 利用FM模型的隐特征向量V作为网络权重初始化来获得子网络输出的embedding向量

这里要注意的一点是,在一些其他DNN做CTR预估的论文当中,会使用预训练的FM模型来进行Deep部分的向量初始化。文中的做法不同,它不是使用训练好的FM来进行初始化,而是和FM模型的部分共享同样的V,将FM和DNN进行整体联合训练,从而实现了一个端到端的模型。
这样做有两个好处
- 它可以同时学习到低维以及高维的特征交叉信息,预训练的FM来进行向量初始化得到的embedding当中可能只包含了二维交叉的信息。
- 这样可以避免像是Wide & Deep那样多余的特征工程。
FM (Factorization Machines)
FM主要是解决稀疏数据下的特征组合问题,并且其预测的复杂度是线性的,对于连续和离散特征有较好的通用性。
FM论文地址
下面是FM二阶部分的数学形式。FM为每个特征学习了一个隐权重向量。在特征交叉时,使用两个向量的内积$\left\langle V{i}, V{j}\right\rangle$作为交叉特征的权重。
本质上,FM引入隐向量的做法,与矩阵分解用隐向量代表用户和物品的做法异曲同工。可以说,FM是将矩阵分解隐向量的思想进行了进一步扩展,从单纯的用户、物品隐向量扩展到了所有特征上。
在工程方面,FM同样可以用梯度下降法进行学习,使其不失实时性和灵活性。相比之后深度学习模型复杂的网络结构导致难以部署和线上服务,FM较容易实现的模型结构使其线上推断的过程相对简单,也更容易进行线上部署和服务。因此,FM在2012一2014年前后,成为业界主流的推荐模型之一。
FM模型优势
在高度稀疏的情况下特征之间的交叉仍然能够估计,而且可以泛化到未被观察的交叉
参数的学习和模型的预测的时间复杂度是线性的
FM更详细介绍见FM(Factorization Machines)的理论与实践
FM部分
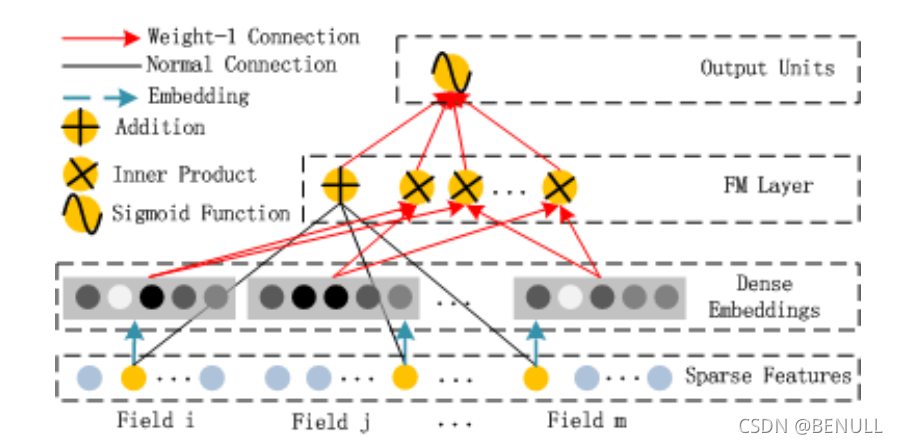
在实践中,FM模块最终是将一阶项与二阶项进行了简单concat。
上图中的Field为特征组,例如性别属性可以看做是一个Field,其有两个特征分别为“男”、“女”。通常来说一个Field中往往只有一个非零特征,但也有可能为多值Field,需要根据实际输入进行适配。
上图的图例中展示了三种颜色的线条,其中绿色的箭头表示为特征的Embedding过程,即得到特征对应的Embedding vector,通常使用 $v_ix_i$ 来表示,而其中的隐向量$v_i$ 则是通过模型学习得到的参数。红色箭头表示权重为1的连接,也就是说红色箭头并不是需要学习的参数。而黑色连线则表示为正常的,需要模型学习的参数$w_i$。
Deep
Deep部分就是经典的前馈网络DNN,用来学习特征之间的高维交叉。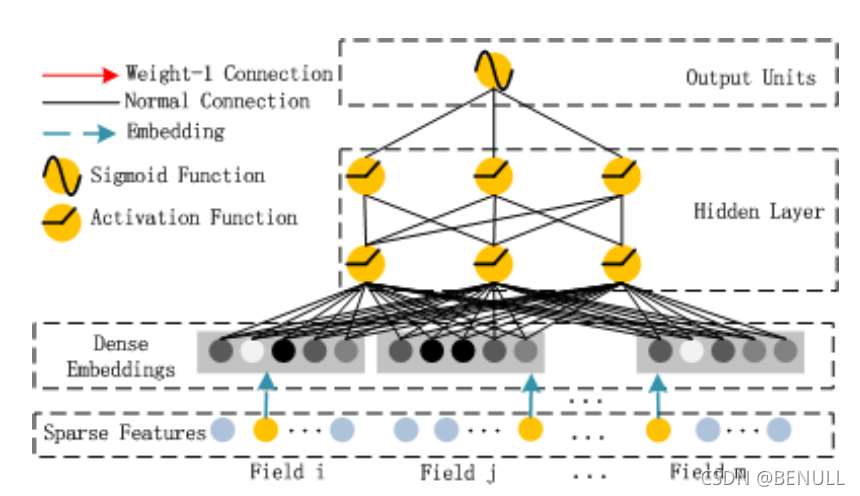
实现
Model
1 | class DeepFM(Model): |
Modules
1 | class FM(Layer): |
参考
- 深度学习推荐系统——王喆
- 深入浅出DeepFM
- 深度推荐模型之DeepFM
- 吃透论文——推荐算法不可不看的DeepFM模型
- Recommender-System-with-TF2.0
- DeepCTR