[异常检测]EXPLAINABLE DEEP ONE-CLASS CLASSIFICATION
会议: 2021 ICLR
论文: https://openreview.net/forum?id=A5VV3UyIQz.
代码:https://github.com/liznerski/fcdd
创新点
因为用于异常检测的深度单分类方法学习映射将正常样本集中在特征空间而将异常样本映射出去。由于这样的变换是非线性的,所以很难去解释。于是这篇文章提出了全卷积数据描述(FCDD),是对DSVDD的一种修改,使变换后的样本本身对应于下采样的异常热力图。
方法
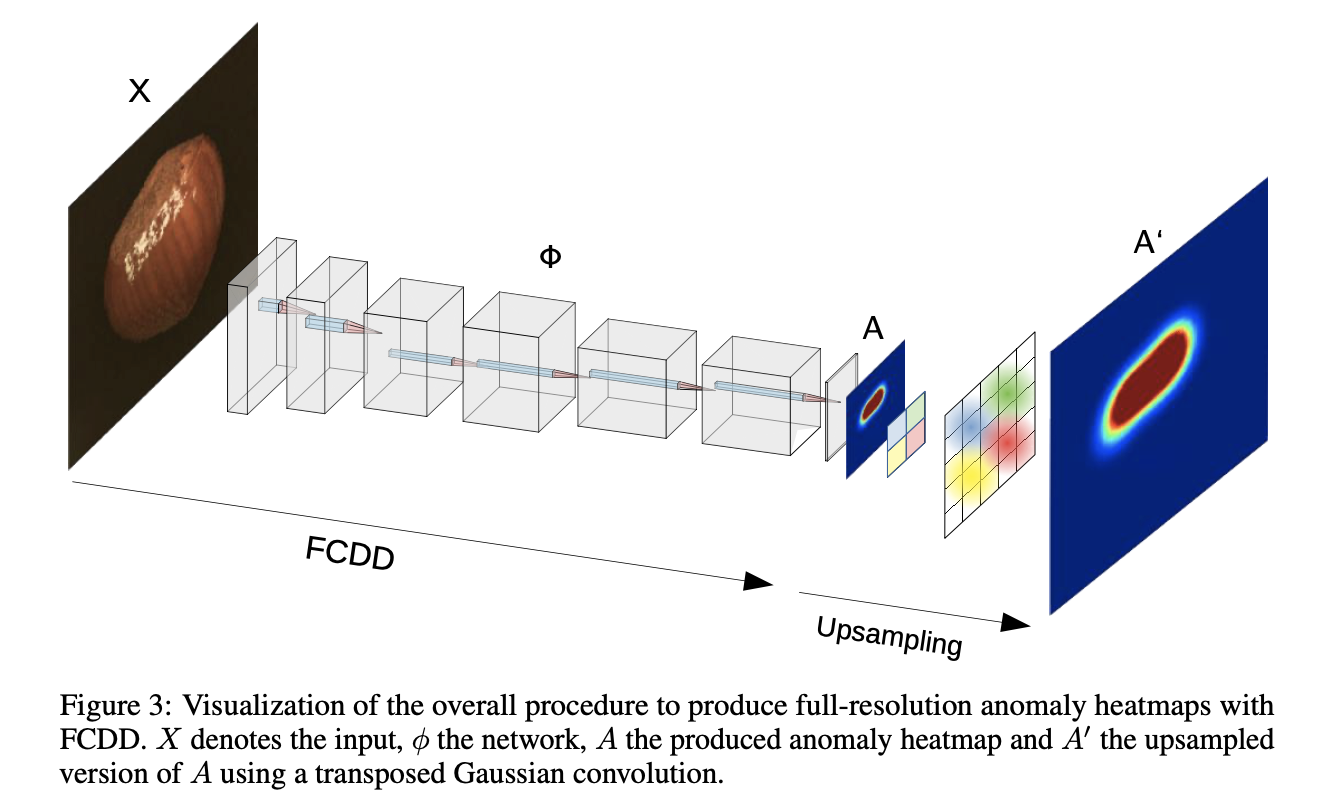
通过FCN全卷积网络,图片被映射到$1 ∗ u ∗ v $的特征图。论文提到卷积层的一个重要性质就是特征图的一个像素只有关于输入的一个固定感受野,这样特征图的异常分数就可以映射回原图片的位置,保留了空间信息。
该方法能够在训练同时给出异常的解释,同时仅使用少量异常样本能显著的提升模型性能。并且使用FCDD的可解释性证明了深度单类分类模型容易受到虚假的图像特征影响(Clever Hans effect)。
同Outlier Exposure的思想一样,文章发现仅使用少数样本作为标记了的异常样本也表现得很出色。此外,在没有任何已知异常的情况下,使用合成异常也是有效的。
FCDD
全卷积数据描述(FCDD),结合FCN和HSC提出了一种深度单分类方法,其中输出特征保留空间信息,同时也作为下采样异常热图。
FCDD目标函数应用Pseudo-Huber 损失函数在FCN的输出矩阵$A(X)=\left(\sqrt{\phi(X ; \mathcal{W})^{2}+1}-1\right)$
目标函数
这里$|A(X)|{1}$是$A(X)$中所有元素的总和,它们都是正的。目标是最大化异常的$|A(X)|{1}$,最小化正常样本的$|A(X)|{1}$,因此使用$|A(X)|{1}$作为异常得分
Huber 损失函数
与平方误差损失相比,对数据中的游离点较不敏感 Huber损失函数经常用于回归问题,它是分段函数,公式如下:
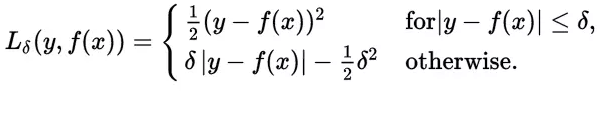
可以看出当残差(预测值与目标值的差值,即y-f(x) )很小的时候,损失函数为L2范数,残差大的时候,为L1范数的线性函数。该公式依赖于参数delta,delta越大,则两边的线性部分越陡峭。
L1、L2、Huber损失函数的对比图如下,其中Huber的delta取0.25、5两个值:
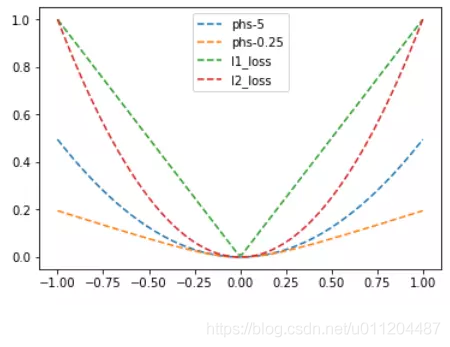
Pseudo-Huber
Huber loss 的一种平滑近似,保证各阶可导

同时对于需要全分辨率热图的情况,提供了一种基于感受野特性对低分辨率热图进行上采样的方法。
Heatmap Upsampling
因为论文的设定在试验阶段是没有ground-truth的,因此上采样部分的训练是无监督的,也就是无法直接训练一个deconvolutional 层所以设计了heatmap upsampling算法

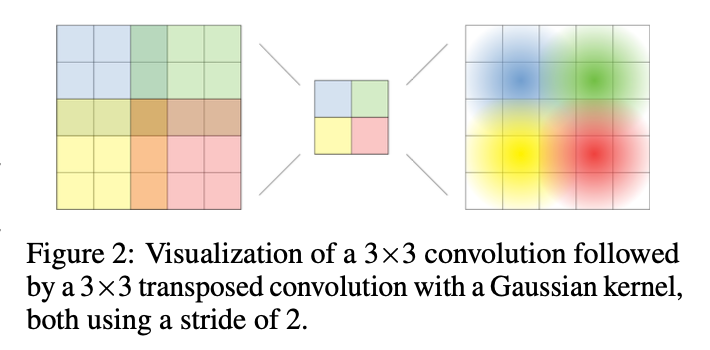
该算法基于feature map的每一个值都对应着原图的唯一一个感受野,并且在该感受野中,每个点对该输出的影响以一种高斯分布从感受野中心进行减弱(想象成一个卷积核的中心的是一个高斯分布的均值点,其他点随着距离下降)
实验